用于计算舵机转向小车前轮转向控制模型的计算

舵机转向小车运动参数解算

编码器每轮783计数

轮子周长 0.2m

编码器计时周期 30ms

编码器长度换算编码器值/4000 m

编码器速度换算编码器值/4000/0.03 m/s

后轮轴长0.16m

前后轮差0.19m

1.后轮电子差速

后轮两个轮子分别使用两个编码器电机通过pid算法可以精确的控制电机转速

车模在转弯时两个后轮走过的路程不一致因此需要差速控制一般汽车上有专业的机械差速器控制差速

差速算法以后再补

2.前轮角度控制

对于一些车模来说前轮是有一个舵机带动而舵机的角度又是会和前轮偏转角度呈一个复杂关系有的车模控制程序简单的用一个线性关系去解算会导致误差较大对舵机连杆进行建模然后通过运动学求解析解就可以得到一个良好的控制模型式

这是我们的控制模型一般来说分为以下两种先考虑第二种

控制原理

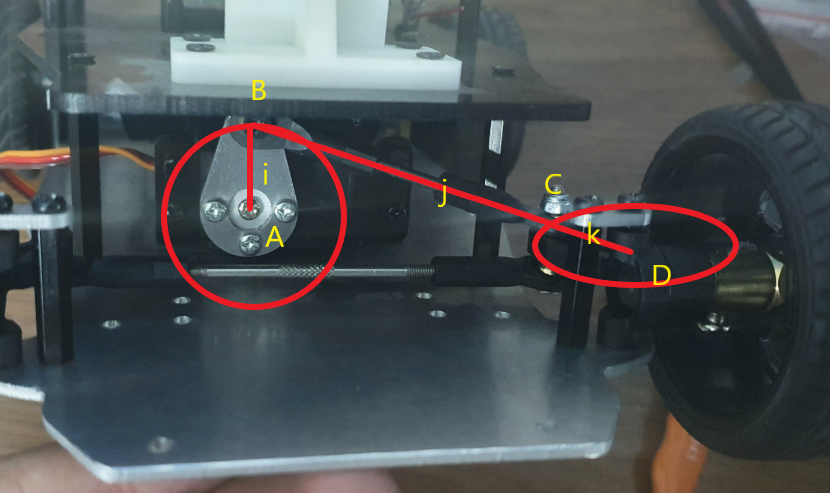
二维绘图

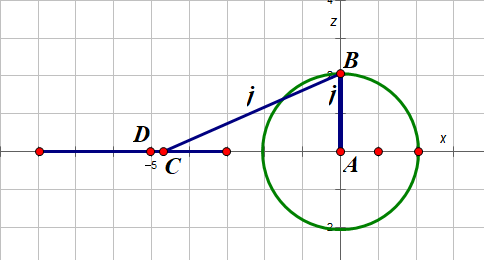
此处AB=i 图画i/j不清楚此处绘制$z_C=z_D=0$实际也可不为零(见下文)

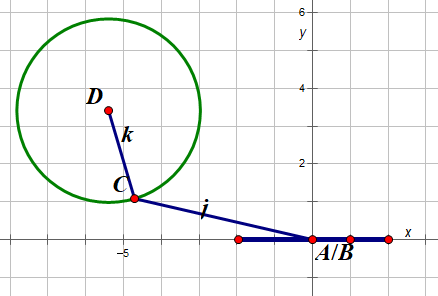
其中圆A和圆D的位置确定圆心和半径可以测量出来 j的长度确定

因此 B和C满足距离公式
$$
(x_B-x_C)^2+(y_B-y_C)^2+(z_B-z_C)^2=j^2①
$$
同时 B和C分别满足圆的公式
$$
x_B^2+z_B^2=i^2②\
y_A=y_B=0(坐标原点设定在A上)\
(x_C-x_D)^2+(y_C-y_D)^2=k^2③\
z_C=z_D
$$
将①展开分别减去②和③ 并带入已知条件可得下式
$$
z_D^2-2x_Bx_C-2z_Bz_C-x_D^2-y_D^2+2x_Cx_D+2y_Cy_D=j^2-k^2-i^2\
2x_Bx_C+2z_Bz_C=i^2-j^2+k^2-x_D^2-y_D^2+z_D^2+2x_Cx_D+2y_Cy_D
$$
如下图做辅助线(2021年12月2日记此处有误投影后BC不为j)

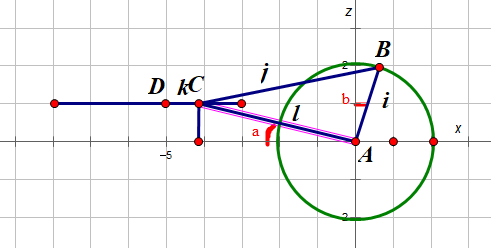
$$
x_C=-l\cos(a)\
z_C=l\sin(a)\
l=\sqrt{x_C^2+z_C^2}\
x_B=i\sin(b)\
z_B=i\cos(b)
$$
带入上式
$$
2il\sin(a)\cos(b)-2il\cos(a)\sin(b)=i^2-j^2+k^2-x_D^2-y_D^2+z_D^2+2x_Cx_D+2y_Cy_D\
\sin(a-b)=\frac{i^2-j^2+k^2-x_D^2-y_D^2+z_D^2+2x_Cx_D+2y_Cy_D}{2il}\
b=a-\arcsin(\frac{i^2-j^2+k^2-x_D^2-y_D^2+z_D^2+2x_Cx_D+2y_Cy_D}{2il})
$$
其中
$$
x_C=x_D+k\sin(c)\
y_C=y_D-k\cos(c)\
z_C=z_D\
a=\arctan(z_C/x_C)\
d-e=c
$$

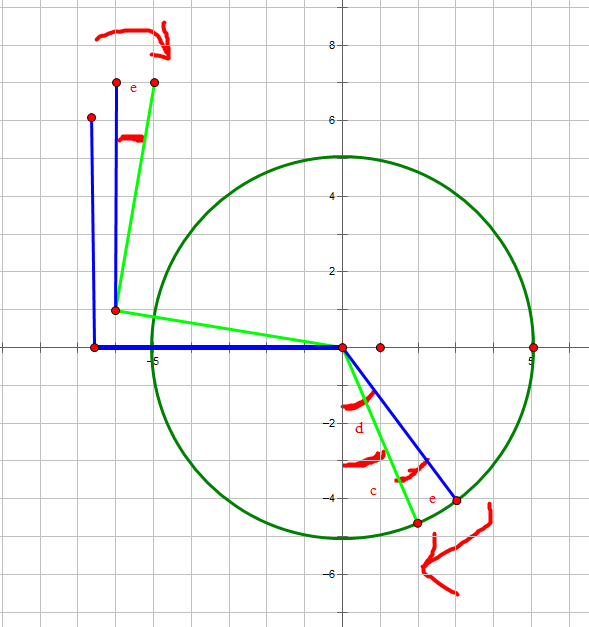
e是轮子的偏转角

d是轮子偏转角为0时 k与y轴负半轴的夹角是结构自带的角度

算法

爷烦了不写了直接贴代码

# -*- coding: utf-8 -*-
"""
Spyder Editor

This is a temporary script file.
"""
import math
import numpy as np
i=0.02
#r2=0
k_y=0.024#y方向长
k_x=0.0045#x方向长
k_z=0#z方向长
k=math.sqrt(k_x**2+k_y**2+k_z**2)
A=(0,0,0)
D_x=-0.063
D_y=0.034
D_z=0
D=(D_x,D_y,D_z) 

C_x_0=D_x+k_x#零位置坐标
C_y_0=D_y-k_y
C_z_0=D_z-k_z
B_x_0=0
B_y_0=0
B_z_0=i

j=math.sqrt((C_x_0-B_x_0)**2+(C_y_0-B_y_0)**2+(C_z_0-B_z_0)**2)

d=math.atan(k_x/k_y)

li=np.zeros(shape=(10001,2))

for tmp in range(-5000,5001,1):
    e=tmp/100/180*math.pi
    c=d-e
    C_x=D_x+math.sin(c)*k
    C_y=D_y-math.cos(c)*k
    C_z=D_z
    a=math.atan(C_z/C_x)
    l=math.sqrt(C_x**2+C_z**2)
    try:
        b=a-math.asin((i**2-j**2+k**2-D_x**2-D_y**2+D_z**2+2*C_x*D_x+2*C_y*D_y)/(2*i*l))
        
        li[tmp+5000,0]=e
        li[tmp+5000,1]=b/math.pi*2000
    except:
        print('err')
    #li.append((tmp/100,b/math.pi*180))
print('ok')
    
drawx=li[:,0]
drawy=li[:,1]

import matplotlib.pyplot as plt
 
#创建绘图图表对象，可以不显式创建，跟cv2中的cv2.namedWindow()用法差不多
plt.figure('Draw')
 
plt.plot(drawy,drawx)
 
plt.draw()

运行结果

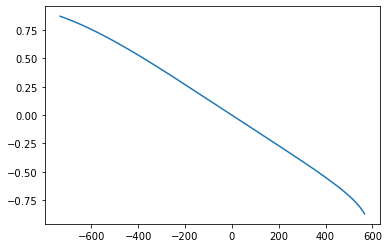
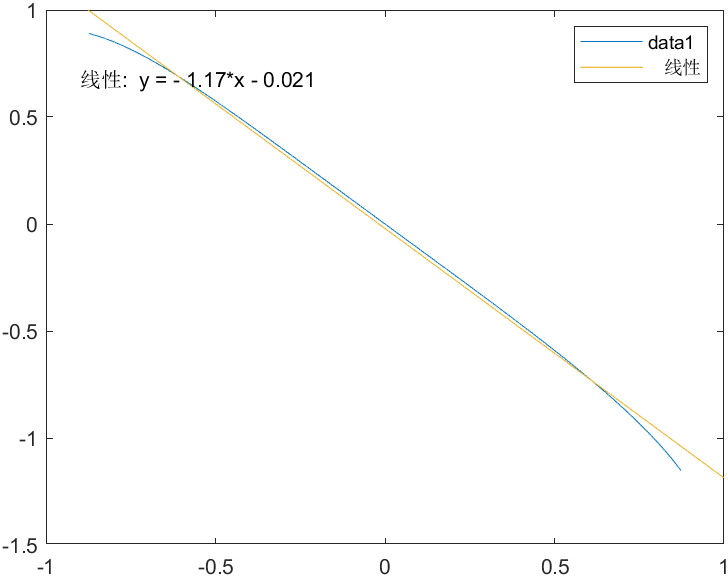
在中间很长一段都有非常好的线性近似直接做个线性就行

以上只考虑了舵机直连轴(左前轮)的运动状况如果要求转向半径可以参考阿克曼转向相关内容